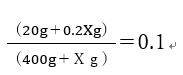「これだけはおさえておきたい!」SPIの7つの基礎計算
「算数」から長い間離れている社会人にとって、問題を解く以前に、
基本的な計算を忘れている方も多いと思います。
そこで、いきなり問題です。
この二つの問題ができない場合は、ぜひ最後までこの記事を読むことを推奨します。
【問題①】
28%が21人でした。
それでは全体(100%)は何人でしょう?
【問題②】
(20g+0.2Xg)/(400g+Xg)=0.1
Xはいくらになるでしょう?
(答えはページ下部にあります。)
簡単すぎるわ!!!と突っこんでいる人は今すぐにブックマークからYoutubeに飛んでくださって問題ないです(笑)
でも、中には算数から長い間離れてしまい
「ヤバい・・・。できないかも」と思っているかもしれません。
このページはそんな方たちを対象に恥ずかしくて質問もできないような簡単な基礎計算問題をしっかりと解説していきます。
題して
「これだけはおさえておきたい!」SPIの7つの基礎計算
逆に言うと、この計算問題さえ解ければ、SPIで出題される問題はクリアできます。
それではさっそく問題です。
【問題①】
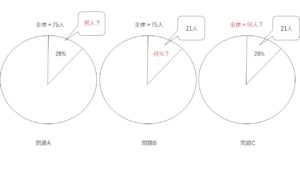
下記の三つの割合問題に対してそれぞれ答えを出すための式を作りなさい
【解答・解説】
<問題A>
こちらは、言語化すると 75人の内28%は何人にあたるか?
という問題に置き換えられます。
したがって、式は 75人×0.28になります。
<問題B>
Bの問題で聞かれている部分は、「割合」になります。
基本的に割合を聞かれている場合は以下の計算式になります。
対象数値÷全体総数
ですから、今回の問題に当てはめると 21人÷75人= 28% となります。
<問題C>
この問題は、「全体総数」を聞いています。
結論から言えば、以下の式で全体総数は出ます。
21人÷0.28(28%)=75人
ここで、「÷0.28」って気持ち悪っ!!! って感じる方が多いかと思います。
しかし、覚えておいて欲しいことは、
少数で割るときには、元に戻す(1=100%)
ということです。
今回の問題で言えば、 21人÷0.28(28%)=75人
28%が21人なら、 元に戻すと(100%)何人になるのか?という意味の式なのです。
【問題②】
下記の計算式から、答えを導きなさい
【解答・解説】
この場合、分母の数が邪魔なので、両辺に分母の数(400+X)を掛け合わせましょう。
すると、
(20+0.2X)=0.1(400+X)
となります。
ここまできたら、右辺の()を外すために0.1をそれぞれ400とXにかけましょう。
0.1(400+X)
すると
40+0.1X
となります。
20+0.2X = 40+0.1X
を計算するときにX同士とX無し同士で分けましょうね。
0.2X+0.1X=40-20
0.1X=20
両辺に10倍かけて(0.1XをXにするために)
X=200となります。
【問題③】
下記の計算式から、答えを導きなさい
1-(1/8+1/2+1/3)=?
【解答・解説】
懐かしいと思いますが、この問題は「通分」ができるかどうかの確認問題です。
覚えていますか?
今回であれば、
(1/8+1/2+1/3)
↑こちらの分母を合わせなければなりません。
1/8の「8」と1/3の「3」を掛け合わせた24が2の倍数になるので、
分母は24になります。
分母を24にするので、
1/8⇒3/24(分子に×3)
1/2⇒12/24(分子に×12)
1/3⇒8/24(分子に×8)
になります。
1-(3/24+12/24+8/24) = 1-23/24
1は24/24なので
24/24-23/24 = 1/24が答えになります。
【問題④】
下記の連立方程式を解き、Yを導きなさい。
X+ Y=1
21X+3Y=18
【解答・解説】
こちらは連立方程式の計算ができるかどうかの確認問題です。
連立方程式の場合、2ステップやることがあります。
(1)聞かれていることの確認(=今回の場合「Y」)
(2)聞かれていない方の数(=「X」についている21)を両辺にかける
よって、
21X+21Y=21
21X+3Y=18
となります。
あとは、上の式と下の式を引き算すれば、
18Y=3
Y=3/18
約分すると1/6になり答えが出ます。
【問題⑤】
以下の計算式を解きなさい。
7P4
【解答・解説】
こちらは場合の数で必ず必要になる計算式です。
答えは、
7×6×5×4=840通りになります
別の問題でやっておくと
5P5は5×4×3×2×1=120通りになります。
【問題⑥】
長さ100mの電車が時速36kmで走っている。
この高速バスが道路わきに立っている人の前を通過するのに何秒かかるか。
ヒント:時速は秒速に直してください
【解答・解説】
「距離・速さ・時間」の問題で必須の計算問題です。
時速を秒速に変換するためには、
(1)時速36kmをメートルに直す
1000mが1kmなので、36kmは36000mになります。
(2)時速36000mを秒速に直す
1時間で36000m進むということなの、1秒だとだいぶ少ない距離しか進めないことをイメージとして持ってくださいね。そうすると、自然と36000m÷3600秒という式が出せるかと思います。(1時間は3600秒)
この計算式を解くと1秒間で10m進むことが分かります。
あとは、100m÷10m/秒=10秒が答えになります。
【問題⑦】
あるたこ焼き屋では値段を30%アップしたら購入者が10%減った。
このときこの売上額は何%増加したか?
【解答・解説】
「率」を聞かれている場合は、数字を計算しやすいもの置き換えてしまいましょう。
料金=100円 購入者=100人と置きます。
①料金を上げる前
100円×100人=10000円
②料金を上げた後
130円×90人=11700円
①と②を比較した時に、売り上げ増加率とは「増加額」÷「増加前の価格」になるので、
(11700円-10000円)÷ 10000円=0.17(17%増加)となります。
はじめの問題の解答
【問題1】75人
【問題2】X=200