SPI対策問題
2019.02.13
転職・昇進者用にSPI厳選8つの問題とその解説を紹介していきたいと思います。
まずは、SPIを受ける上でのメンタリティーを説明させていただきます。
SPIの非言語問題は、転職において唯一
「地頭の良さ」を測るものになります。
経歴や成績なんて、実はいくらでもごまかせちゃいますが、
SPIの検査では、ごまかせません。
成績が良くても、小学生ができる問題がズタボロだと、
「こいつ大丈夫?」ってなってしまいます。
そうならないために、しっかりと出題問題と出題レベルを抑えていきましょう。
それでは、転職者向けの「SPI-G」では、どのような問題が出るのか?
ランキング順位でご紹介します。
出題ランキング
推論
制限時間: 2分
A、B、C、D、Eの5人が身長を測定した。5人の身長について次のことが分かっている。
CはDより身長が高い
Eの身長はDより低いが、Eよりも身長が低い人がいた
AはBより身長が高い
同じ身長の人はいない
次のア、イ、ウの推論のうち、必ず正しいものはどれか。(複数回答可能)
ア. Bは最も身長が低い
イ. Cは最も身長が高い
ウ. 2番目に身長が低いのはAまたはEである
【解答・解説】
ポイント①
「必ず正しいものはどれか」
このような聞かれ方をしたときは、難易度は比較的簡単なので、時間がかかりそうだとしても必ず最後まで取り掛かりましょう。
ポイント②
推論の問題は与えられた条件で、すべての情報が確定するわけではない。
これは結構大事で、多くの人が、以下のように与えられている条件で
個々のすべての順位が分かると誤解しています。
実は、以下の条件数では、すべての個々の人の順位が決まるためには不十分なケースの方が多いので、無理に、順位をピッタリと決める必要はありません。
CはDより身長が高い
Eの身長はDより低いが、Eよりも身長が低い人がいた
AはBより身長が高い
同じ身長の人はいない
では上から順に整理していきます。
「CはDより身長が高い」

「Eの身長はDより低いが、Eよりも身長が低い人がいた」

この時点で、合計人数は、5人なので、
Eより低い人は、AかBのどちらかになります。
「AはBより身長が高い」
この時点で、Bが最も低いとわかります。

ここまでの情報で、Aが何番目なのかについて、確定できる情報がありません。
故に、B以外の人たちが具体的に何番目かはわかりません。
さて、選択肢を一つ一つ吟味していきましょう。
ア.Bは最も身長が高い
⇒これは正しいですね。Bが最も身長が低いです。
イ.Cは最も身長が高い
⇒これはダメです。その理由は、Aが最も身長が高い可能性が残されているため、必ず正しいとは言い切れません。
ウ.2番目に身長が低いのはAまたはEである
⇒これは正しいですね。AはBより身長が高いですが、Bの次に高い可能性もあるのでこの選択肢は正しいです。
答え:アとウ
損益算
制限時間: 1分
田中さんはデパートのセールの初日に定価の3割引きで服を買い,
鈴木さんは同じ服をセール最終日に定価の6割引きで購入した。
田中さんと鈴木さんの購入額の差額は2100円だった。
この服の定価はいくらか?
【解答・解説】
はじめに定価を決めて3割引きとしました。
ですので、購入額の70%分(3割を定価から引く)を田中さんは支払ったことになります。
さらに、最終日は6割引きしたので以下の式になります。
0.7X – 4X = 2100円
0.3X=2100円
答え:7000円
確率
制限時間: 1分
5人の中から1人罰ゲームを決める時、
5本のうち1本ハズレが入っているくじを順番にひく。
3番目にくじを引く人が罰ゲームになる確率を答えなさい
ただし引いたくじは元にもどさない
【解答・解説】
最初の人がはずれの確率→4/5
次の人もはずれの確率→3/4
3番目の人の当たる確率→1/3
これらをかければよいので、
4/5×3/4×1/3=1/5になります。
答え:1/5
仕事算
制限時間: 1分
ある仕事をするのに田中さんは6日間、鈴木さんは10日間で仕上げる。
2人で一緒にすると何日目で仕事を終えることができるか?
【解答・解説】
仕事算は「仕事」÷「能力」=「時間」で解くことが出来ます。
そして仕事全体を「1」と置きます。そうすると田中さんは6日かかるので、
1÷6日= 田中さんの能力は1/6(一日当たりに1/6の仕事を進められる)
鈴木さんの能力は1/10(一日当たりに1/10の仕事を進められる)
2人で仕事全体=「1」を
終わらせるので、一日当たりの二人の仕事の能力を出します。
※仕事は「2」になりません!!!!
そうすると田中さんの能力1/6+ 鈴木さんの能力1/10=4/15になります。
(一日当たりに4/15の仕事を進められる)
したがって1÷ 4/15=15/4(3.75)
3日目を過ぎているので答えは4日目に終わるが正解です。
答え:4日目
距離・速さ・時間
制限時間: 1分
田中さんは自宅から3.5km離れた美術館まで,行きは自転車で平均時速10.5km/時で走りました。
帰りはチェーンが外れてしまい、走って帰った。すると、往復するのに50分かかった。
帰りの時速はどのくらいか?
【解答・解説】
距離を速さで割ることで、“必要な時間”が出せます。
3.5km ÷ 10.5km/時 = 1/3時間(つまり20分)を要したことになります。
全体では、50分かかったとあるので、行きに要した20分を引くと、
帰りは、30分要したことになります。
聞かれているところは、帰りの速さになるので、計算式は以下になります。
距離 ÷ 速さ = 時間
3.5km ÷ Xkm/時 = 30分
しかしここで注意。 速さの単位は「1時間」になっているのに、時間の単位は「分」になってしまっています。
単位を必ず、合わせましょう!
ではどちらに合わせるか?
この場合は、52分⇒30/60時間としましょう。
ですので、正しい式は以下になります。
3.5km ÷ Xkm/時 = 1/2時間
これを解くと、x=7km/時 となります。
答え:7km/時
分割払い
制限時間: 1分
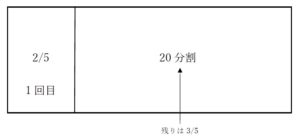
田中さんはスポーツカーを購入した。一括購入が難しかったため、支払いは21回の分割払いとし,購入時に1回目として代金の2/5を支払うことにした。
また、2回目以降は均等に支払うことにした。
4回目の支払いが済んだ時点で支払い済みの額は総額のどれだけにあたるか。
※分割払いの手数料や利子は考えないものとする。
【解答・解説】

上記のように、1回目として代金の2/5を支払っているので、
残金は、3/5となります。
それを20分割(ここを21としてはダメ!)するので、
3/5 ÷ 20 = 3/100
答え:3/100
割合・比
制限時間: 1分
箱の中にみかんといちごの個数が7:5の割合で入っていた。この中からいちごの1/3にあたる3個をもらった。
このとき箱の中に入っていたみかんは何個か?
【解答・解説】

みかんといちごの個数が7:5=全体を7+5の12と置きます。
そうすると、いちごは全体の5/12となります。
そこから、 5/12のうちの1/3、つまり1/36が3個ということになるので、
3個÷1/36=108個が全体の数だということが分かります。
みかんは全体の7/12なので、答えは108×7/12の63個です。
答え:63個
方角・地図の縮図
制限時間: 1分
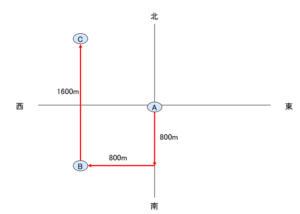
A小学校から真南に800m進み、直角に左折してやはり800m進むとB中学校がある。また、B中学校から真北に1.6km進むとC高校がある。
(1)B中学校は、A小学校から見てどの方角にあたるか。
A. 東 B. 西 C. 南 D. 北
E. 南東 F. 南西 G. 北東 H. 北西
(2) この区域を縮尺1/5000の地図で見ると、A小学校とB中学校結ぶ直線を対角線とする正方形の一辺の長さは何cmになるか。
A. 0.4cm B. 0.8cm
C. 3.6cm D. 4.0cm
E. 8.0cm F. 32.0cm
G. 40.0cm H. A~Gのいずれでもない
【解答・解説】
(1)以下の図のような動きになるので、Hの「北西」が正しい答えになります。

(2) 「A小学校とB中学校結ぶ直線を対角線とする正方形の一辺の長さ」は800mです。
縮尺1/2500の地図では、800m÷2500=80000cm÷2500=32cm。
答え:Fの32cm